The globe was there, the pennies were there. The Tissot Indicatrix file was somewhere else. Where's the glue?!
Compare the pennies on the globe with their approximations in Web Mercator. The penny island way up near the North Pole is the same penny you see down around Central America, but look at the resulting size warp! You might notice, too, that the pennies get increasingly bulgy at their top and start looking teardrop-shaped. That is because over the north-south distance of the penny island the scale factor has increased that much. In fact, as you approach the North Pole the vertical stretching approaches infinity.
The imaginary islands that look a lot like pennies. Check out what Web Mercator has done to them!
Shoot, while I'm at it let me illustrate Great Circle lines real quick. Here's me snapping a straight line between two locations on the surface of the Earth. If I could fly and was in a hurry, this is the path I would take. But actual straight lines arc in the Mercator projection. Check it out:
That photograph above shows me snapping a straight line on the Earth. When I warp that image into the Mercator projection you get a sense of how actual straight lines bend in Mercator (and vice-versa).
Web Mercator is becoming such a de-facto projection that I'm pretty sure that our zeitgeisty collective thinks of it as the actual shape of the earth. Yeah yeah, I know it's passé to pick on Mercator, and I suppose I am a bit, but it's important we keep this understanding of scale trade-off rattling around. So behold these globe-hack illustrations!
Gerardus, forgive me; I am indebted to your mathematical and entrepreneurial skills. I can't stay mad at you.
Tweet Follow @JohnNelsonIDV Follow @IDVSolutions
P.S. I used to think that Mercator "maintained straight lines"; that straight lines in real life were straight in Mercator. But they are not -I misunderstood that so many years ago in my foolish misspent youth. What they really let navigators do, and why the projection was such a hit in the 1500's, was let sailors draw straight lines on the map which represented rhumb lines in real life. Rhumb lines aren't actually straight but as long as you sailed at the same angle on the ship's magnetic compass, you'd eventually get where you wanted to go (which was way better than dead reckoning). Here's more on rhumb lines, otherwise awesomely known to Mad Maxians as loxodromes.
Keep your bearing! Full sail! Source: Wikipedia.





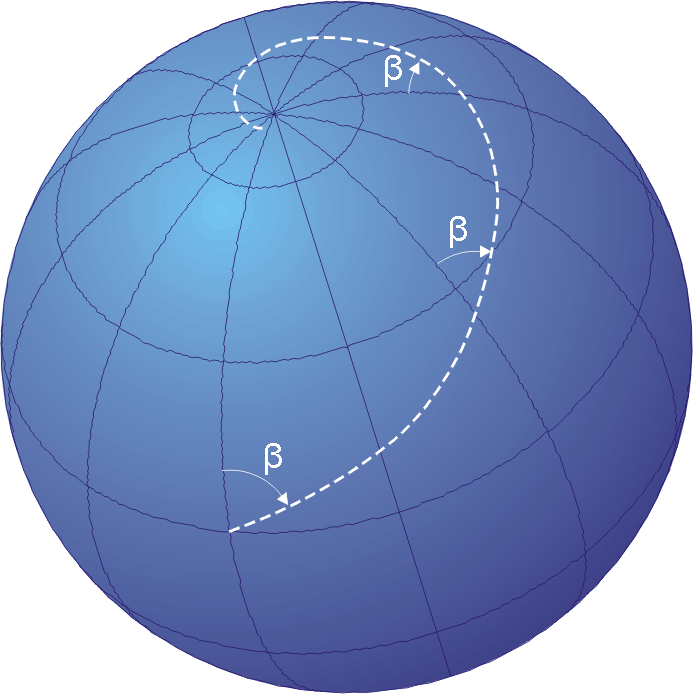
Wow. Sailing back then must have been really confusing.
ReplyDeleteBut your illustrations are so clear and understandable. :)
ReplyDeleteThanks Matt. Though it did cost me eight cents.
Delete